前面的话
本文将详细介绍图这种数据结构,包含不少图的巧妙运用
数据结构
图是网络结构的抽象模型。图是一组由边连接的节点(或顶点)。图是重要的,因为任何二元关系都可以用图来表示
任何社交网络,例如Facebook、Twitter和Google plus,都可以用图来表示。还可以使用图来表示道路、航班以及通信状态,如下图所示:
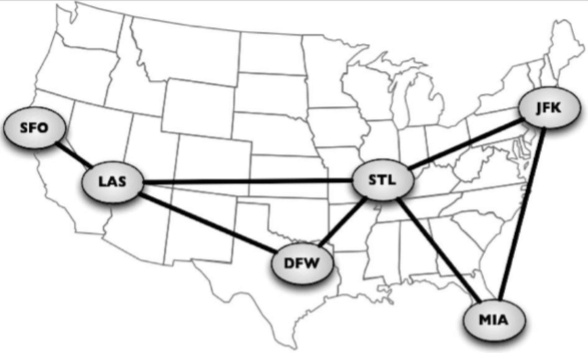
一个图G = (V, E)由以下元素组成
V:一组顶点E:一组边,连接V中的顶点
下图表示一个图:
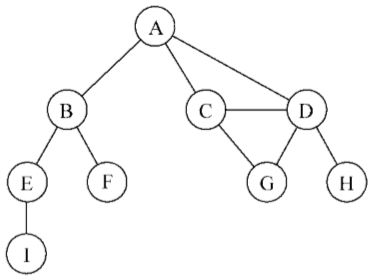
在着手实现算法之前,先了解一下图的一些术语
由一条边连接在一起的顶点称为相邻顶点。比如,A和B是相邻的,A和D是相邻的,A和C是相邻的,A和E不是相邻的。
一个顶点的度是其相邻顶点的数量。比如,A和其他三个顶点相连接,因此,A的度为3;E和其他两个顶点相连,因此,E的度为2。
路径是顶点v1,v2,…,vk的一个连续序列,其中vi和vi+1是相邻的。以上一示意图中的图为例,其中包含路径A B E I和A C D G。
简单路径要求不包含重复的顶点。举个例子,ADG是一条简单路径。除去最后一个顶点(因为它和第一个顶点是同一个顶点),环也是一个简单路径,比如ADCA(最后一个顶点重新回到A)
如果图中不存在环,则称该图是无环的。如果图中每两个顶点间都存在路径,则该图是连通的
【有向图和无向图】
图可以是无向的(边没有方向)或是有向的(有向图)。如下图所示,有向图的边有一个方向:
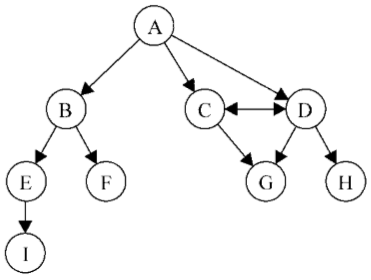
如果图中每两个顶点间在双向上都存在路径,则该图是强连通的。例如,C和D是强连通的,而A和B不是强连通的。
图还可以是未加权的(目前为止我们看到的图都是未加权的)或是加权的。如下图所示,加权图的边被赋予了权值:

可以使用图来解决计算机科学世界中的很多问题,比如搜索图中的一个特定顶点或搜索一条特定边,寻找图中的一条路径(从一个顶点到另一个顶点),寻找两个顶点之间的最短路径,以及环检测
图的表示
从数据结构的角度来说,有多种方式来表示图。在所有的表示法中,不存在绝对正确的方式。图的正确表示法取决于待解决的问题和图的类型
【邻接矩阵】
图最常见的实现是邻接矩阵。每个节点都和一个整数相关联,该整数将作为数组的索引。我 们用一个二维数组来表示顶点之间的连接。如果索引为i的节点和索引为j的节点相邻,则array[i][j] === 1,否则array[i][j] === 0,如下图所示:
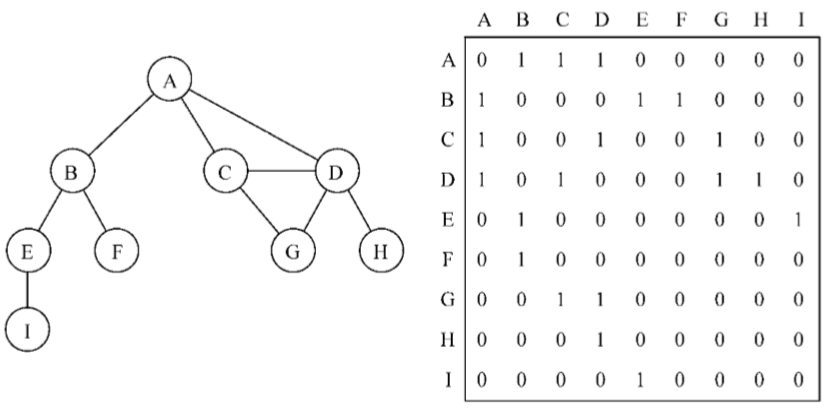
不是强连通的图(稀疏图)如果用邻接矩阵来表示,则矩阵中将会有很多0,这意味着我们浪费了计算机存储空间来表示根本不存在的边。例如,找给定顶点的相邻顶点,即使该顶点只有一个相邻顶点,我们也不得不迭代一整行。邻接矩阵表示法不够好的另一个理由是,图中顶点的数量可能会改变,而2维数组不太灵活
【邻接表】
也可以使用一种叫作邻接表的动态数据结构来表示图。邻接表由图中每个顶点的相邻顶点列表所组成。存在好几种方式来表示这种数据结构。我们可以用列表(数组)、链表,甚至是散列表或是字典来表示相邻顶点列表。下面的示意图展示了邻接表数据结构
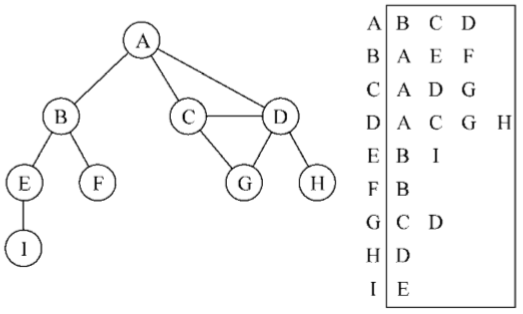
尽管邻接表可能对大多数问题来说都是更好的选择,但以上两种表示法都很有用,且它们有着不同的性质(例如,要找出顶点v和w是否相邻,使用邻接矩阵会比较快)
【关联矩阵】
还可以用关联矩阵来表示图。在关联矩阵中,矩阵的行表示顶点,列表示边。如下图所示,使用二维数组来表示两者之间的连通性,如果顶点v是边e的入射点,则array[v][e] === 1; 否则,array[v][e] === 0
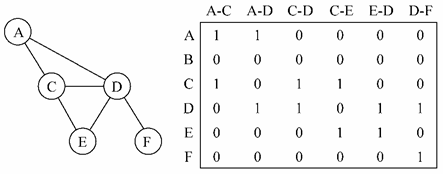
关联矩阵通常用于边的数量比顶点多的情况下,以节省空间和内存
创建Graph类
声明类的骨架:
function Graph() { var vertices = []; //{1} var adjList = new Dictionary(); //{2}} 使用一个数组来存储图中所有顶点的名字(行{1}),以及一个字典来存储邻接表(行{2})。字典将会使用顶点的名字作为键,邻接顶点列表作为值。vertices数组和adjList字典两者都是我们Graph类的私有属性
接着,将实现两个方法:一个用来向图中添加一个新的顶点(因为图实例化后是空的),另外一个方法用来添加顶点之间的边
先实现addVertex方法:
this.addVertex = function(v){ vertices.push(v); //{3} adjList.set(v, []); //{4}}; 这个方法接受顶点v作为参数。将该顶点添加到顶点列表中(行{3}),并且在邻接表中,设置顶点v作为键对应的字典值为一个空数组(行{4})
现在,来实现addEdge方法:
this.addEdge = function(v, w){ adjList.get(v).push(w); //{5} adjList.get(w).push(v); //{6}}; 这个方法接受两个顶点作为参数。首先,通过将w加入到v的邻接表中,添加了一条自顶点v到顶点w的边。如果想实现一个有向图,则行{5}就足够了。如果是基于无向图的,需要添加一条自w向v的边(行{6})
下面来测试这段代码:
var graph = new Graph();var myVertices = ['A','B','C','D','E','F','G','H','I']; //{7}for (var i=0; i 为方便起见,创建了一个数组,包含所有想添加到图中的顶点(行{7})。接下来,只要遍历vertices数组并将其中的值逐一添加到我们的图中(行{8})。最后,添加想要的边(行{9})。这段代码将会创建一个图,也就是到前面的示意图所使用的
为了更方便一些,下面来实现一下Graph类的toString方法,以便于在控制台输出图
this.toString = function(){ var s = ''; for (var i=0; i '; var neighbors = adjList.get(vertices[i]); //{11} for (var j=0; j 我们为邻接表表示法构建了一个字符串。首先,迭代vertices数组列表(行{10}),将顶点的名字加入字符串中。接着,取得该顶点的邻接表(行{11}),同样也迭代该邻接表(行{12}),将相邻顶点加入我们的字符串。邻接表迭代完成后,给我们的字符串添加一个换行符(行{13}),这样就可以在控制台看到一个漂亮的输出了。运行如下代码:
console.log(graph.toString());
输出如下:
A -> B C D B -> A E F C -> A D GD -> A C G H E -> B IF -> BG -> C D H -> DI -> E
从该输出中,顶点A有这几个相邻顶点:B、C和D
图的遍历
和树数据结构类似,可以访问图的所有节点。有两种算法可以对图进行遍历:广度优先搜索(Breadth-First Search,BFS)和深度优先搜索(Depth-First Search,DFS)。图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径,检查图是否连通,检查图是否含有环等
在实现算法之前,需要理解图遍历的思想方法。图遍历算法的思想是必须追踪每个第一次访问的节点,并且追踪有哪些节点还没有被完全探索。对于两种图遍历算法,都需要明确指出第一个被访问的顶点
完全探索一个顶点要求我们查看该顶点的每一条边。对于每一条边所连接的没有被访问过的顶点,将其标注为被发现的,并将其加进待访问顶点列表中
为了保证算法的效率,务必访问每个顶点至多两次。连通图中每条边和顶点都会被访问到
广度优先搜索算法和深度优先搜索算法基本上是相同的,只有一点不同,那就是待访问顶点列表的数据结构
算法 数据结构 描 述深度优先搜索 栈 通过将顶点存入栈中,顶点是沿着路径被探索的,存在新的相邻顶点就去访问广度优先搜索 队列 通过将顶点存入队列中,最先入队列的顶点先被探索
当要标注已经访问过的顶点时,用三种颜色来反映它们的状态
白色:表示该顶点还没有被访问。灰色:表示该顶点被访问过,但并未被探索过。黑色:表示该顶点被访问过且被完全探索过。
这就是之前提到的务必访问每个顶点最多两次的原因
【广度优先搜索】
广度优先搜索算法会从指定的第一个顶点开始遍历图,先访问其所有的相邻点,就像一次访问图的一层。换句话说,就是先宽后深地访问顶点,如下图所示:
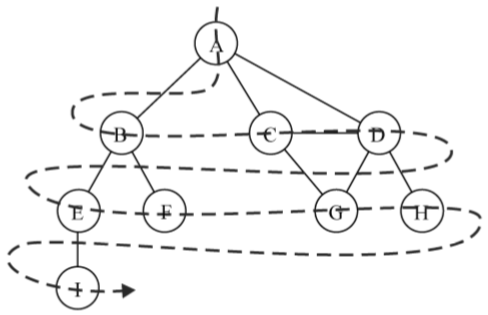
以下是从顶点v开始的广度优先搜索算法所遵循的步骤
(1) 创建一个队列Q。
(2) 将v标注为被发现的(灰色),并将v入队列Q。 (3) 如果Q非空,则运行以下步骤: (a) 将u从Q中出队列; (b) 将标注u为被发现的(灰色); (c) 将u所有未被访问过的邻点(白色)入队列; (d) 将u标注为已被探索的(黑色)下面来实现广度优先搜索算法:
var initializeColor = function(){ var color = []; for (var i=0; i 广度优先搜索和深度优先搜索都需要标注被访问过的顶点。为此,将使用一个辅助数组color。由于当算法开始执行时,所有的顶点颜色都是白色(行{1}),所以可以创建一个辅助函数initializeColor,为这两个算法执行此初始化操作
下面来深入广度优先搜索方法的实现。要做的第一件事情是用initializeColor函数来将color数组初始化为white(行{2})。还需要声明和创建一个Queue实例(行{3}),它将会存储待访问和待探索的顶点。bfs方法接受一个顶点作为算法的起始点。起始顶点是必要的,将此顶点入队列(行{4})。如果队列非空(行{5}),将通过出队列(行{6})操作从队列中移除一个顶点,并取得一个包含其所有邻点的邻接表(行{7})。该顶点将被标注为grey(行{8}),表示发现了它(但还未完成对其的探索)。
对于u(行{9})的每个邻点,取得其值(该顶点的名字——行{10}),如果它还未被访问过(颜色为white——行{11}),则将其标注为已经发现了它(颜色设置为grey——行{12}),并将这个顶点加入队列中(行{13}),这样当其从队列中出列的时候,可以完成对其的探索。当完成探索该顶点 和其相邻顶点后,将该顶点标注为已探索过的(颜色设置为black——行{14})
实现的这个bfs方法也接受一个回调。这个参数是可选的,如果传递了回调函数(行{15}),会用到它。执行下面这段代码来测试一下这个算法:
function printNode(value){ //{16} console.log('Visited vertex: ' + value); //{17}}graph.bfs(myVertices[0], printNode); //{18} 首先,声明了一个回调函数(行{16}),它仅仅在浏览器控制台上输出已经被完全探索过的顶点的名字。接着,调用bfs方法,给它传递第一个顶点(A——myVertices数组)和回调函数。执行这段代码时,该算法会在浏览器控制台输出下示的结果:
Visited vertex: A Visited vertex: B Visited vertex: C Visited vertex: D Visited vertex: E Visited vertex: F Visited vertex: G Visited vertex: H Visited vertex: I
顶点被访问的顺序和示意图中所展示的一致
考虑如何来解决下面这个问题。给定一个图G和源顶点v,找出对每个顶点u,u和v之间最短路径的距离(以边的数量计)。 对于给定顶点v,广度优先算法会访问所有与其距离为1的顶点,接着是距离为2的顶点,以此类推。所以,可以用广度优先算法来解这个问题。可以修改bfs方法以返回给我们一些信息:
从v到u的距离d[u];前溯点pred[u],用来推导出从v到其他每个顶点u的最短路径。
下面是改进过的广度优先方法的实现:
this.BFS = function(v){ var color = initializeColor(), queue = new Queue(), d = [], //{1} pred = []; //{2} queue.enqueue(v); for (var i=0; i 还需要声明数组d(行{1})来表示距离,以及pred数组来表示前溯点。下一步则是对图中的每一个顶点,用0来初始化数组d(行{4}),用null来初始化数组pred。发现顶点u的邻点w时,则设置w的前溯点值为u(行{7})。还通过给d[u]加1来设置v和w之间的距离(u是w的前溯点,d[u]的值已经有了)。方法最后返回了一个包含d和pred的对象(行{8})
现在,可以再次执行BFS方法,并将其返回值存在一个变量中:
var shortestPathA = graph.BFS(myVertices[0]); console.log(shortestPathA);
对顶点A执行BFS方法,以下将会是输出:
distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3],predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G:"C", H: "D", I: "E"]
这意味着顶点A与顶点B、C和D的距离为1;与顶点E、F、G和H的距离为2;与顶点I的距离为3。通过前溯点数组,可以用下面这段代码来构建从顶点A到其他顶点的路径:
var fromVertex = myVertices[0]; //{9}for (var i=1; i 用顶点A作为源顶点(行{9})。对于每个其他顶点(除了顶点A——行{10}),会计算顶点A到它的路径。从顶点数组得到toVertex(行{11}),然后会创建一个栈来存储路径值(行{12})。接着,追溯toVertex到fromVertex的路径{行{13}}。变量v被赋值为其前溯点的值,这样能够反向追溯这条路径。将变量v添加到栈中(行{14})。最后,源顶点也会被添加到栈中,以得到完整路径。
这之后,创建了一个s字符串,并将源顶点赋值给它(它是最后一个加入栈中的,所以它是第一个被弹出的项 ——行{16})。当栈是非空的,就从栈中移出一个项并将其拼接到字符串s的后面(行{18})。最后(行{19})在控制台上输出路径。执行该代码段,会得到如下输出:
A - BA - CA - DA - B - EA - B - FA - C - GA - D - HA - B - E - I
这里,得到了从顶点A到图中其他顶点的最短路径(衡量标准是边的数量)
如果要计算加权图中的最短路径(例如,城市A和城市B之间的最 短路径——GPS和Google Maps中用到的算法),广度优先搜索未必合适。
举些例子,Dijkstra’s算法解决了单源最短路径问题。Bellman–Ford算法解决了边权值为负的单源最短路径问题。A*搜索算法解决了求仅一对顶点间的最短路径问题,它用经验法则来加速搜索过程。Floyd–Warshall算法解决了求所有顶点对间的最短路径这一问题。
图是一个广泛的主题,对最短路径问题及其变种问题,有很多的解决方案。但在开始学习这些其他解决方案前,需要掌握好图的基本概念
【深度优先搜索】
深度优先搜索算法将会从第一个指定的顶点开始遍历图,沿着路径直到这条路径最后一个顶点被访问了,接着原路回退并探索下一条路径。换句话说,它是先深度后广度地访问顶点,如下图所示:
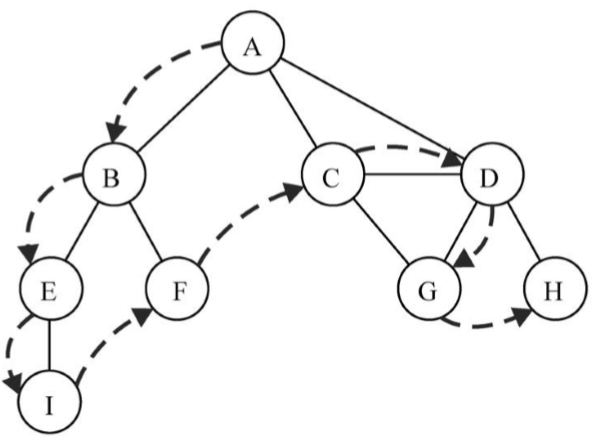
深度优先搜索算法不需要一个源顶点。在深度优先搜索算法中,若图中顶点v未访问,则访问该顶点v。要访问顶点v,照如下步骤做
1、标注v为被发现的(灰色)。
2、对于v的所有未访问的邻点w,访问顶点w,标注v为已被探索的(黑色)
深度优先搜索的步骤是递归的,这意味着深度优先搜索算法使用栈来存储函数调用(由递归调用所创建的栈)
下面来实现一下深度优先算法:
this.dfs = function(callback){ var color = initializeColor(); //{1} for (var i=0; i 首先,创建颜色数组(行{1}),并用值white为图中的每个顶点对其做初始化,广度优先搜索也这么做的。接着,对于图实例中每一个未被访问过的顶点(行{2}和{3}),调用私有的递归函数dfsVisit,传递的参数为顶点、颜色数组以及回调函数(行{4})
当访问u顶点时,标注其为被发现的(grey——行{5})。如果有callback函数的话(行{6}),则执行该函数输出已访问过的顶点。接下来一步是取得包含顶点u所有邻点的列表(行{7})。对于顶点u的每一个未被访问过(颜色为white——行{10}和行{8})的邻点w(行{9}), 将调用dfsVisit函数,传递w和其他参数(行{11}——添加顶点w入栈,这样接下来就能访问它)。最后,在该顶点和邻点按深度访问之后,我们回退,意思是该顶点已被完全探索,并将其标注为black(行{12})
执行下面的代码段来测试一下dfs方法:
graph.dfs(printNode);
输出如下:
Visited vertex: A Visited vertex: B Visited vertex: E Visited vertex: I Visited vertex: F Visited vertex: CVisited vertex: D Visited vertex: G Visited vertex: H
这个顺序和示意图所展示的一致。下面这个示意图展示了该算法每一步的执行过程:

行{4}只会被执行一次,因为所有其他的顶点都有路径到第一个调用dfsVisit函数的顶点(顶点A)。如果顶点B第一个调用函数,则行{4}将会为其他顶点再执行一次(比如顶点A)
到目前为止,只是展示了深度优先搜索算法的工作原理。可以用该算法做更多的事情,而不只是输出被访问顶点的顺序
对于给定的图G,希望深度优先搜索算法遍历图G的所有节点,构建“森林”(有根树的一个集合)以及一组源顶点(根),并输出两个数组:发现时间和完成探索时间。可以修改dfs方法来返回一些信息:
顶点u的发现时间d[u];当顶点u被标注为黑色时,u的完成探索时间f[u];顶点u的前溯点p[u]。
来看看改进了的DFS方法的实现:
var time = 0; //{1} this.DFS = function(){ var color = initializeColor(), //{2} d = [], f = [], p = []; time = 0; for (var i=0; i 需要一个变量来要追踪发现时间和完成探索时间(行{1})。时间变量不能被作为参数传递,因为非对象的变量不能作为引用传递给其他JavaScript方法(将变量作为引用传递的意思是如果该变量在其他方法内部被修改,新值会在原始变量中反映出来)。接下来,声明数组d、f和p(行{2})。需要为图的每一个顶点来初始化这些数组(行{3})。在这个方法结尾处返回这些值(行{4}),之后要用到它们
当一个顶点第一次被发现时,追踪其发现时间(行{5})。当它是由引自顶点u的边而被发现的,追踪它的前溯点(行{6})。最后,当这个顶点被完全探索后,追踪其完成时间(行{7})
深度优先算法背后的思想是什么?边是从最近发现的顶点u处被向外探索的。只有连接到未发现的顶点的边被探索了。当u所有的边都被探索了,该算法回退到u被发现的地方去探索其他的边。这个过程持续到发现了所有从原始顶点能够触及的顶点。如果还留有任何其他未被发现的顶点,对新源顶点重复这个过程。重复该算法,直到图中所有的顶点都被探索了
对于改进过的深度优先搜索,有两点需要注意
1、时间(time)变量值的范围只可能在图顶点数量的一倍到两倍之间
2、对于所有的顶点u,d[u]<f[u](意味着,发现时间的值比完成时间的值小,完成时间意思是所有顶点都已经被探索过了)
在这两个假设下,有如下的规则:
1≤d[u]
如果对同一个图再跑一遍新的深度优先搜索方法,对图中每个顶点,会得到如下的发现
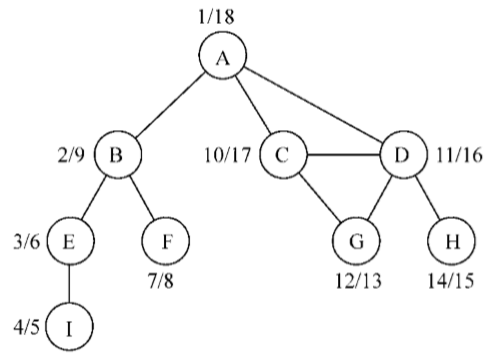
给定下图,假定每个顶点都是一个需要去执行的任务:
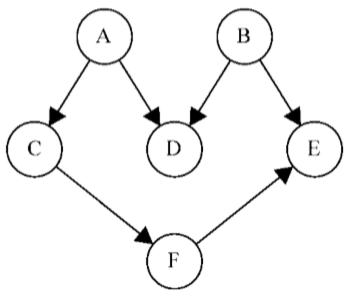
这是一个有向图,意味着任务的执行是有顺序的。例如,任务F不能在任务A之前执行。这个图没有环,意味着这是一个无环图。所以,可以说该图是一个有向无环图(DAG)
当需要编排一些任务或步骤的执行顺序时,这称为拓扑排序(topologicalsorting,英文亦写作topsort或是toposort)。在日常生活中,这个问题在不同情形下都会出现。例如,开始学习一门计算机科学课程,在学习某些知识之前得按顺序完成一些知识储备(不可以在上算法I前先上算法II)。在开发一个项目时,需要按顺序执行一些步骤,例如,首先得从客户那里得到需求,接着开发客户要求的东西,最后交付项目。不能先交付项目再去收集需求
拓扑排序只能应用于DAG。那么,如何使用深度优先搜索来实现拓扑排序呢?在前面的示意图上执行一下深度优先搜索
graph = new Graph();myVertices = ['A','B','C','D','E','F'];for(i=0;i
这段代码将创建图,添加边,执行改进版本的深度优先搜索算法,并将结果保存到result变量。下图展示了深度优先搜索算法执行后,该图的发现和完成时间
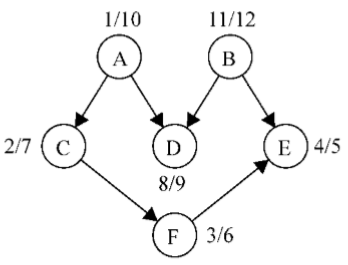
现在要做的仅仅是以倒序来排序完成时间数组,这便得出了该图的拓扑排序:
B - A - D - C - F - E
注意之前的拓扑排序结果仅是多种可能性之一。如果稍微修改一下算法,就会有不同的结果,比如下面这个结果也是众多其他可能性中的一个:
A - B - C - D - F - E
这也是一个可以接受的结果
【完整代码】
Graph类的完整代码如下所示
function Graph() { var vertices = []; //list var adjList = new Dictionary(); this.addVertex = function(v){ vertices.push(v); adjList.set(v, []); //initialize adjacency list with array as well; }; this.addEdge = function(v, w){ adjList.get(v).push(w); //adjList.get(w).push(v); //commented to run the improved DFS with topological sorting }; this.toString = function(){ var s = ''; for (var i=0; i '; var neighbors = adjList.get(vertices[i]); for (var j=0; j
最短路径算法
设想要从街道地图上的A点,通过可能的最短路径到达B点。这种问题在生活中非常常见,会求助于百度地图等应用程序。当然,也有其他的考虑,如时间或路况,但根本的问题仍然是: 从A到B的最短路径是什么?
可以用图来解决这个问题,相应的算法被称为最短路径。下面将介绍两种非常著名的算法,即Dijkstra算法和Floyd-Warshall算法
【Dijkstra算法】
Dijkstra算法是一种计算从单个源到所有其他源的最短路径的贪心算法,这意味着可以用它来计算从图的一个顶点到其余各顶点的最短路径
考虑下图:
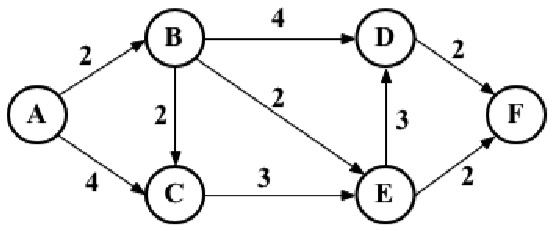
下面来看看如何找到顶点A和其余顶点之间的最短路径。但首先,需要声明表示上图的邻接矩阵,如下所示:
var graph = [[0, 2, 4, 0, 0, 0], [0, 0, 1, 4, 2, 0], [0, 0, 0, 0, 3, 0], [0, 0, 0, 0, 0, 2], [0, 0, 0, 3, 0, 2], [0, 0, 0, 0, 0, 0]];
现在,通过下面的代码来看看Dijkstra算法是如何工作的:
this.dijkstra = function(src) { var dist = [], visited = [], length = this.graph.length; for (var i = 0; i < length; i++) { //{1} dist[i] = INF; visited[i] = false; } dist[src] = 0; //{2} for (var i = 0; i < length-1; i++) { //{3} var u = minDistance(dist, visited); //{4} visited[u] = true; //{5} for (var v = 0; v < length; v++) { if (!visited[v] && this.graph[u][v] != 0 && dist[u] != INF && dist[u] + this.graph[u][v] < dist[v]) { //{6} dist[v] = dist[u] + this.graph[u][v]; //{7} } } } return dist; //{8} }; 下面是对算法过程的描述
行{1}:首先,把所有的距离(dist)初始化为无限大(JavaScript最大的数INF = Number. MAX_SAFE_INTEGER),将visited[]初始化为false
行{2}:然后,把源顶点到自己的距离设为0
行{3}:接下来,要找出到其余顶点的最短路径
行{4}:为此,需要从尚未处理的顶点中选出距离最近的顶点
行{5}:把选出的顶点标为visited,以免重复计算
行{6}:如果找到更短的路径,则更新最短路径的值(行{7})
行{8}:处理完所有顶点后,返回从源顶点(src)到图中其他顶点最短路径的结果
要计算顶点间的minDistance,就要搜索dist数组中的最小值,返回它在数组中的索引:
var minDistance = function(dist, visited) { var min = INF, minIndex = -1; for (var v = 0; v < dist.length; v++) { if (visited[v] == false && dist[v] <= min) { min = dist[v]; minIndex = v; } } return minIndex;}; 对前面的图执行以上算法,会得到如下输出:
0 01 22 33 64 45 6
【Floyd-Warshall算法】
Floyd-Warshall算法是一种计算图中所有最短路径的动态规划算法。通过该算法,可以找出从所有源到所有顶点的最短路径
Floyd-Warshall算法实现如下:
this.floydWarshall = function() { var dist = [], length = this.graph.length, i, j, k; for (i = 0; i < length; i++) { //{1} dist[i] = []; for (j = 0; j < length; j++) { dist[i][j] = this.graph[i][j]; } } for (k = 0; k < length; k++) { //{2} for (i = 0; i < length; i++) { for (j = 0; j < length; j++) { if (dist[i][k] + dist[k][j] < dist[i][j]) { //{3} dist[i][j] = dist[i][k] + dist[k][j]; //{4} } } } } return dist; }; 下面是对算法过程的描述
行{1}:首先,把dist数组初始化为每个顶点之间的权值,因为i到j可能的最短距离就是这些顶点间的权值
行{2}:通过k,得到i途径顶点0至k,到达j的最短路径
行{3}:判断i经过顶点k到达j的路径是否比已有的最短路径更短
行{4}:如果是更短的路径,则更新最短路径的值
行{3}是Floyd-Warshall算法的核心。对前面的图执行以上算法,会得到如下输出:
0 2 3 6 4 6 INF 0 1 4 2 4 INF INF 0 6 3 5 INF INF INF 0 INF 2 INF INF INF 3 0 2 INF INF INF INF INF 0
其中,INF代表顶点i到j的最短路径不存在。 对图中每一个顶点执行Dijkstra算法,也可以得到相同的结果
最小生成树
最小生成树(MST)问题是网络设计中常见的问题。想象一下,公司有几间办公室,要以最低的成本实现办公室电话线路相互连通,以节省资金,最好的办法是什么?这也可以应用于岛桥问题。设想要在n个岛屿之间建造桥梁,想用最低的成本实现所有岛屿相互连通
这两个问题都可以用MST算法来解决,其中的办公室或者岛屿可以表示为图中的一个顶点,边代表成本。下面有一个图的例子,其中较粗的边是一个MST的解决方案
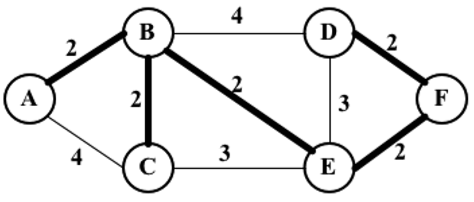
下面将介绍两种主要的求最小生成树的算法:Prim算法和Kruskal算法
【Prim算法】
Prim算法是一种求解加权无向连通图的MST问题的贪心算法。它能找出一个边的子集,使得其构成的树包含图中所有顶点,且边的权值之和最小
现在,通过下面的代码来看看Prim算法是如何工作的:
this.prim = function() { var parent = [], key = [], visited = [], length = this.graph.length, i; for (i = 0; i < length; i++){ key[i] = INF; visited[i] = false; } key[0] = 0; parent[0] = -1; for (i = 0; i < length-1; i++) { var u = minKey(key, visited); visited[u] = true; for (var v = 0; v < length; v++){ if (this.graph[u][v] && visited[v] == false && this.graph[u][v] < key[v]){ parent[v] = u; key[v] = this.graph[u][v]; } } } return parent;}; 下面是对算法过程的描述
行{1}:首先,把所有顶点(key)初始化为无限大(JavaScript最大的数INF = Number.MAX_ SAFE_INTEGER),visited[]初始化为false
行{2}:其次,选择第一个key作为第一个顶点,同时,因为第一个顶点总是MST的根节点,所以parent[0] = -1
行{3}:然后,对所有顶点求MST
行{4}:从未处理的顶点集合中选出key值最小的顶点(与Dijkstra算法中使用的函数一样, 只是名字不同)
行{5}:把选出的顶点标为visited,以免重复计算
行{6}:如果得到更小的权值,则保存MST路径(parent,行{7})并更新其权值(行 {8})
行{9}:处理完所有顶点后,返回包含MST的结果
比较Prim算法和Dijkstra算法,会发现除了行{7}和行{8}之外,两者非常相似。行{7}用parent数组保存MST的结果。行{8}用key数组保存权值最小的边,而在Dijkstra算法中,用dist数组保存距离。可以修改Dijkstra算法,加入parent数组。这样,就可以在求出距离的同时得到路径
对如下的图执行以上算法:
var graph = [[0, 2, 4, 0, 0, 0], [2, 0, 2, 4, 2, 0], [4, 2, 0, 0, 3, 0], [0, 4, 0, 0, 3, 2], [0, 2, 3, 3, 0, 2], [0, 0, 0, 2, 2, 0]];
会得到如下输出:
Edge Weight 0 - 1 2 1 - 2 2 5 - 3 2 1 - 4 2 4 - 5 2
【Kruskal算法】
和Prim算法类似,Kruskal算法也是一种求加权无向连通图的MST的贪心算法。现在,通过下面的代码来看看Kruskal算法是如何工作的:
this.kruskal = function(){ var length = this.graph.length, parent = [], cost, ne = 0, a, b, u, v, i, j, min; cost = initializeCost(); while(ne < length; i++) { for(j=0;j < length; j++) { if(cost[i][j] < min) { min=cost[i][j]; a = u = i; b = v = j; } } } u = find(u, parent); v = find(v, parent); if (union(u, v, parent)){ ne++; } cost[a][b] = cost[b][a] = INF; } return parent;} 下面是对算法过程的描述
行{1}:首先,把邻接矩阵的值复制到cost数组,以方便修改且可以保留原始值行{7}
行{2}:当MST的边数小于顶点总数减1时
行{3}:找出权值最小的边
行{4}和行{5}:检查MST中是否已存在这条边,以避免环路
行{6}:如果u和v是不同的边,则将其加入MST
行{7}:从列表中移除这些边,以免重复计算
行{8}:返回MST
下面是find函数的定义。它能防止MST出现环路:
var find = function(i, parent){ while(parent[i]){ i = parent[i]; } return i;}; union函数的定义如下:
var union = function(i, j, parent){ if(i != j) { parent[j] = i; return true; } return false;}; 这个算法有几种变体。这取决于对边的权值排序时所使用的数据结构(如优先队列),以及图是如何表示的